E, AP con:
E= parte entera
A= ante período
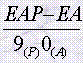
P= período
Los números decimales son una forma de expresar cantidades que no son enteras, se escriben con una coma seguida de cifras que representan partes de la unidad: décimas, centésimas, milésimas, etc, siguiendo las mismas reglas de nuestro sistema decimal que da a cada cifra su valor de posición:
|
… |
Millares |
Centenas |
Decenas |
unidades |
décimas |
centésimas |
milésimas |
… |
|
… |
1000 |
100 |
10 |
1 |
0.1 |
0.01 |
0.001 |
… |
Todos los números racionales se pueden escribir en forma decimal dividiendo el numerador entre el denominador siempre obtendremos un decimal exacto o periódico.
Los números decimales exactos se escriben como fracción poniendo en el numerador el número que resulta de quitar la coma y en el denominador, la unidad seguida de tantos ceros como cifras hay después de la coma.
Los decimales periódicos pueden ser puros, si se repiten todos los números después de la coma o mixtos si hay una parte decimal no incluida en el periodo.
Se pueden representar:
|
E, AP con:
|
E= parte entera |
La fracción generatriz será: |
|
A= ante período |
|
|
|
P= período |
Ejemplos:
|
0,0045 = |
|
= |
|
![]()
![]()
Además podemos escribir números decimales que no se pueden representar con una fracción, no son exactos ni periódicos, son los números irracionales, tienen una cantidad infinita de cifras decimales que no se repiten de forma periódica.
Algunos de los números más importantes de la Historia de las matemáticas son irracionales, por ejemplo Pi:
p = 3,141592653589793…
Si te p-ca la curiosidad aquí tienes hasta 5.000.000 de decimales:
http://www.geocities.com/Baja/Trails/4422/pi/
![]()
El lenguaje algebraico. Ecuaciones
Una expresión en la que aparecen números y letras enlazados mediante operaciones aritméticas es una expresión algebraica.
Una ecuación es una igualdad de dos expresiones algebraicas y resolverla consiste en encontrar todos los valores de las letras que hacen que esa igualdad sea cierta.
Generalmente para resolver una ecuación la iremos transformando en otras ecuaciones equivalentes más sencillas hasta dar con la solución. Para ello podemos utilizar las siguientes propiedades:
![]() P1
Al sumar o restar la
misma cantidad a los dos miembros de una ecuación se obtiene otra equivalente.
P1
Al sumar o restar la
misma cantidad a los dos miembros de una ecuación se obtiene otra equivalente.
![]() P2
Al multiplicar o dividir por la misma cantidad los dos miembros
de una ecuación se obtiene otra equivalente.
P2
Al multiplicar o dividir por la misma cantidad los dos miembros
de una ecuación se obtiene otra equivalente.
![]()
Ecuaciones de primer grado con una incógnita
Se llaman ecuaciones lineales.
El método general de resolución consiste en reducirla a una de la forma
ax=b
que resolvemos directamente:
![]() Si a¹0,
la única solución es x=b/a
Si a¹0,
la única solución es x=b/a
![]() Si
a=0 y b¹0
no existe solución
Si
a=0 y b¹0
no existe solución
![]() Si
a=b=0 cualquier número es solución.
Si
a=b=0 cualquier número es solución.
Los métodos para resolver ecuaciones datan de los tiempos de los babilonios (2000 a.C.).
Método general :
![]() Eliminamos paréntesis:
Eliminamos paréntesis:
Si hay, eliminamos todos los niveles de paréntesis que aparezcan, comenzando por el más interno, resolviendo las operaciones indicadas.
![]() Eliminamos denominadores:
Eliminamos denominadores:
Si hay, eliminamos todos los denominadores, reduciendo primero todos los términos a denominador común y luego multiplicando por este valor ambos lados de la ecuación. Este paso es opcional, si se prefiere se puede trabajar con las fracciones y despejar al final.
![]() Agrupamos términos semejantes:
Agrupamos términos semejantes:
Agrupamos las expresiones con la variable en un lado y las expresiones numéricas en el otro y operamos en cada uno de ellos.
![]() Despejamos la variable
Despejamos la variable
Despejamos la variable, obteniendo así la solución.
![]() Comprobamos la solución
Comprobamos la solución
Comprobamos si la solución satisface la ecuación propuesta, es decir si aparece una identidad verdadera.
Ejemplos
|
1
|
2
|
|
3
|
4
|
![]()
Ecuaciones de segundo grado
Son aquellas que después de quitar paréntesis y reducir términos semejantes quedan de la forma
ax2 + bx + c = 0
|
Y se resuelven usando la fórmula: |
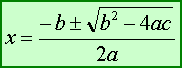 |
La expresión que está debajo de la raíz se llama discriminante, y se representa D y el número de soluciones de la ecuación depende de él:
Si D > 0 la ecuación tiene dos soluciones (una para + y otra para –)
Si D < 0 la ecuación no tiene solución real (tendríamos la raíz cuadrada de un número negativo)
Si D = 0 la ecuación sólo tiene una solución (decimos que es una solución doble)
Si una ecuación de segundo grado no está completa, es decir no aparecen todos los términos, se puede resolver más fácilmente sin usar la fórmula:
Caso 1 ( b = 0 ):
ax2 + c = 0
ax2 = – c
x2 = – c /a
|
x = |
|
Caso 2 (c = 0 ):
ax2 + bx = 0
x·( ax + b ) = 0
solución 1: x = 0
solución 2: ( ax + b ) = 0
x = – b /a
|
Si quieres saber más: |
 |
![]()
Sistemas de ecuaciones
Un sistema de ecuaciones es un conjunto formado por varias ecuaciones y resolverlo consiste en encontrar los valores de las incógnitas que hacen que todas ellas sean ciertas a la vez.
De nuevo, para resolver un sistema de ecuaciones lo iremos transformando en otro equivalente más sencillo hasta dar con la solución. Para ello podemos utilizar las mismas propiedades de las ecuaciones ( P1 y P2) y además:
![]() P3
Al sustituir
una de las ecuaciones por su suma o su diferencia con otra obtenemos un sistema
equivalente.
P3
Al sustituir
una de las ecuaciones por su suma o su diferencia con otra obtenemos un sistema
equivalente.
Sistemas de dos ecuaciones lineales con dos incógnitas.
Son de la forma:
![]()
Ejemplo:
![]()
La solución es el par (x, y) = ( 3, 2) vamos a obtenerla por tres métodos:
Métodos de resolución:
Método de sustitución
Consiste en despejar una incógnita en una de las ecuaciones y sustituir su valor en la otra.
|
Despejamos x en la 1ª ecuación |
x = 7 – 2y |
|
Sustituimos el valor de x en la 2ª ecuación |
2(7 – 2y) – y = 4 |
|
Operamos en la 2ª ecuación para calcular y |
14 – 4y – y = 4 Þ 14 – 4 = 5y Þ y = 10 / 5 = 2 |
|
Sustituimos el valor de y en la 1ª ecuación |
x = 7 – 2 ·2 = 3 |
Método de igualación
Consiste en despejar la misma incógnita en ambas ecuaciones y después igualar los resultados:
|
Despejamos x en la 1ª ecuación |
x = 7 – 2y |
|
Despejamos x en la 2ª ecuación |
x = |
|
Igualamos ambos valores y operamos |
|
|
Sustituimos el valor de y en una de las ecuaciones |
x = 7 – 2 ·2 = 3 |
Método de reducción
Consiste en multiplicar si es necesario cada ecuación por un número para que al sumar las dos ecuaciones desaparezca una incógnita.
|
Multiplicamos la 2ª ecuación por 2 |
4x – 2 y = 8 |
|
Sumamos las dos ecuaciones |
|
|
Sustituimos el valor de x en una de las ecuaciones |
3 + 2 y = 7 Þ 2 y = 4Þ y = 2 |
![]()
|
|
Hipotenusa : c Catetos : a y b Proyección del cateto a = a’ Proyección del cateto b = b’ Altura : h Ángulos agudos : a yb |
|
|
RELACIONES MÉTRICAS |
||
|
Teorema de PITÁGORAS: |
a2 + b2 = c2 |
|
|
Teorema de la altura: |
h2 = a’ · b’ |
|
|
Teorema del cateto: |
a2 = a’ · c y b2 = b’ · c |
|
|
RELACIONES TRIGONOMÉTRICAS |
||
|
Seno = |
Cat. opuesto |
Sen a = |
a |
Sen b = |
b |
|
hipotenusa |
c |
c |
|||
|
Coseno = |
Cat. contiguo |
Cos a = |
b |
Cos b = |
a |
|
hipotenusa |
c |
c |
|||
|
Tangente = |
Cat. opuesto |
Tg a = |
a |
Tg b = |
b |
|
Cat. contiguo |
b |
a |
|
Triángulos (cualesquiera) |
|||||||||||||
|
CÁLCULO DEL ÁREA |
|||||||||||||
|
|
||||||||||||
|
Fórmula de HERÓN |
|
||||||||||||
|
RESOLVER UN TRIÁNGULO |
|||||||||||||
|
Resolver un triángulo cualquiera consiste en calcular sus tres lados y sus tres ángulos. |
|||||||||||||
|
Para resolver un triángulo debemos conocer, al menos, tres de sus elementos, uno de los cuales necesariamente debe ser un lado. |
|||||||||||||
| La suma de los ángulos de un triángulo es 180º | |||||||||||||
![]()
|
Ángulos agudos:
En el triángulo rectángulo dado, se definen: |
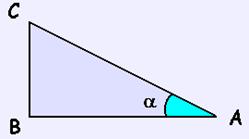 |
|
Seno = |
Cat. opuesto |
Sen a = |
CB |
||
|
hipotenusa |
AC |
||||
|
Coseno = |
Cat. contiguo |
Cos a = |
AB |
||
|
hipotenusa |
AC |
||||
|
Tangente = |
Cat. opuesto |
Tg a = |
CB |
= |
Sen a |
|
Cat. contiguo |
AB |
Cos a |
|||
|
Ángulos cualesquiera: Se considera en la circunferencia U, el punto (x,y) corte con la semirrecta dada por el ángulo a, definimos: |
|
|
sen
a=
y Cos a=x |
tg a= |
|
Relaciones entre las razones trigonométricas:
|
Tg a = |
|
sen2a + cos2 a = 1 |
![]()