Arquímedes de Siracusa 287 AC, 212 AC Siracusa, Sicilia

Arquímedes era un nativo de Siracusa, (actual Italia, h. 287 a.C.-id., 212 a.C.) Matemático griego. Hijo de un astrónomo, quien probablemente le introdujo en las matemáticas, Arquímedes estudió en Alejandría, donde tuvo como maestro a Conón de Samos y entró en contacto con Eratóstenes; a este último dedicó Arquímedes su Método, en el que expuso su genial aplicación de la mecánica a la geometría, en la que «pesaba» imaginariamente áreas y volúmenes desconocidos para determinar su valor. Regresó luego a Siracusa, donde se dedicó de lleno al trabajo científico.y estudió en Alejandría, volviendo en seguida a su patria. Dedicó su genio a la geometría, mecánica, física e Ingeniería.
Aunque las mayores contribuciones de Arquímedes fueron en geometría, sus métodos de cálculo integral se anticiparon 2.000 años a Newton y Leibniz.

De la biografía de Arquímedes, gran matemático e ingeniero, a quien Plutarco atribuyó una «inteligencia sobrehumana», sólo se conocen una serie de anécdotas. La más divulgada la relata Vitruvio y se refiere al método que utilizó para comprobar si existió fraude en la confección de una corona de oro encargada por Hierón II, tirano de Siracusa y protector de Arquímedes, quizás incluso pariente suyo. Hallándose en un establecimiento de baños, advirtió que el agua desbordaba de la bañera a medida que se iba introduciendo en ella; esta observación le inspiró la idea que le permitió resolver la cuestión que le planteó el tirano. Se cuenta que, impulsado por la alegría, corrió desnudo por las calles de Siracusa hacia su casa gritando «Eureka! Eureka!», es decir, «¡Lo encontré! ¡Lo encontré!».

Escribió varias obras las cuales se han ordenado según la época en que fueron escritas:
1. Esfera y cilindro.
2. Medida del círculo.
3. Gnoides y esferoides.
4. Espirales.
5. Equilibrio de los planos y sus centros de gravedad.
6. Cuadratura de la parábola.
7. El arenario.
8. Cuerpos flotantes.
9. Los lemas.
10. El método.

Arquímedes demostró que la superficie de una esfera es cuatro veces la de uno de sus círculos máximos. Calculó áreas de zonas esféricas y el volumen de segmentos de una esfera. Demostró que " El área de un casquete esférico es igual a la superficie de un círculo que tiene por radio la recta que une el centro del casquete con punto de la circunferencia basal".

El problema al cual le atribuía gran importancia era el de demostrar que "El volumen de una esfera inscrita en un cilindro es igual a 2/3 del volumen del cilindro". Como postrer homenaje se colocó una esfera inscrita en un cilindro. Asimismo demostró Arquímedes que la superficie de esta esfera era también los 2/3 de la superficie del cilindro.

Es tal vez más interesante su trabajo sobre Medida del circulo. Trata de la rectificación de la circunferencia y el área del círculo. Arquímedes es el primero que hizo un intento verdaderamente positivo sobre el cálculo de p=Pí asignándole un valor entre 3(10/71)

El método que empleó consiste en calcular los perímetros de los polígonos regulares inscritos y circunscritos a un mismo círculo.

Admite, sin demostrarlos, los principios siguientes:

1. " La línea recta es la más corta entre 2 puntos."
2. " De 2 líneas cóncavas hacia el mismo lado y que tienen los mismos extremos, es mayor la que queda fuera de la otra".- ó como diríamos ahora " es mayor la línea circundante que la circundada". Este principio lo aplica al círculo y a los polígonos inscritos y circunscritos"
3. " De 2 superficies que pasan por una misma curva cerrada, cóncavas hacia un mismo lado, es mayor la exterior."

También demuestra que "un círculo es equivalente a un triángulo que tiene por base la circunferencia y por altura el radio."

ARQUÍMEDES Y EL VOLUMEN DE LA ESFERA

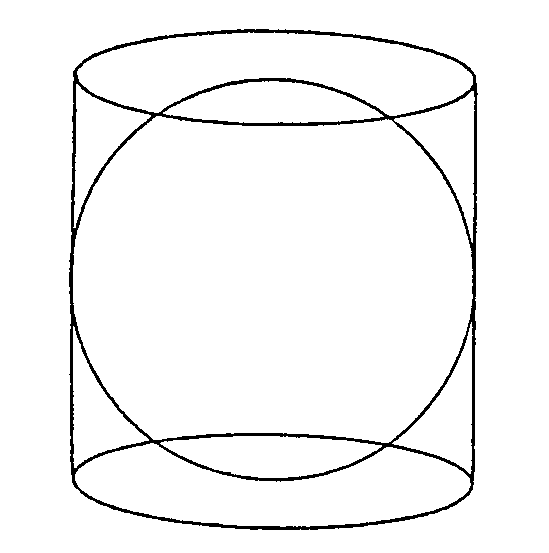Muchos conocen al sabio Arquímedes, especialmente por las palancas. El cálculo del volumen de la esfera fue uno de los descubrimientos que Arquímedes más estimaba de todos los que hizo en su vida. Llegó a demostrar de un modo muy original que el volumen de la esfera es igual a dos tercios del volumen del cilindro circular circunscrito a ella. Tanto le impresionó esto a él mismo (tal vez porque en ese entonces se hablaba de los cuerpos perfectos) que mandó que en su tumba se grabase esta figura en recuerdo de la mejor de sus ideas.

Veamos cómo llegó a este interesante descubrimiento.

Arquímedes se imaginó una semiesfera y junto a ella un cilindro circular recto y un cono recto, ambos de base igual a un círculo máximo de la semiesfera. Algo parecido al dibujo que te mostramos

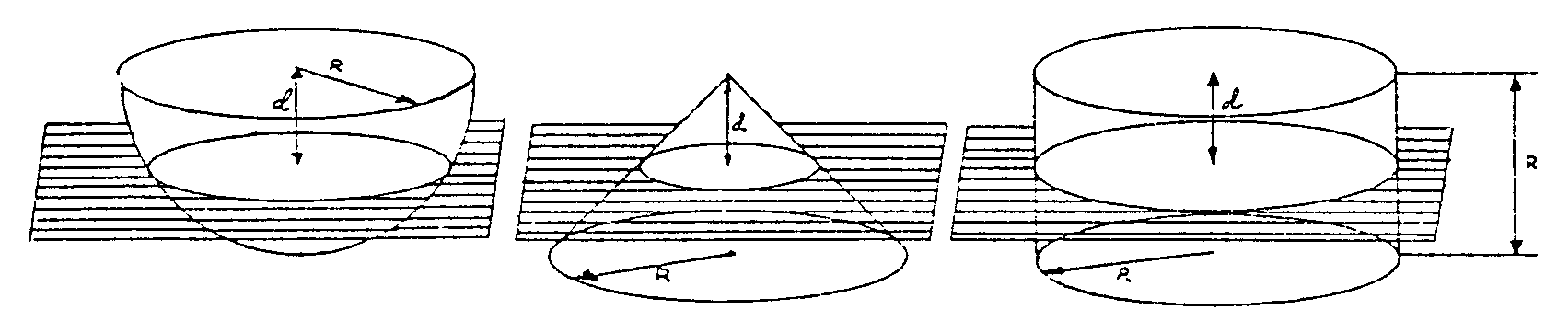
Arquímedes cortó las tres figuras por un plano paralelo a la base del cilindro y el cono y se preguntó cómo serían las secciones determinadas por este plano en cilindro, semiesfera y cono.

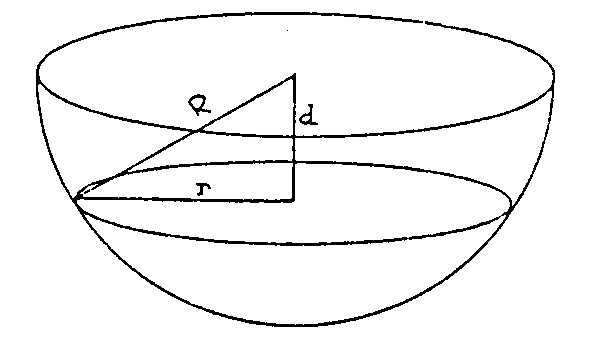
En el cilindro se obtiene un círculo de radio R (no olvides que el radio es la mitad del diámetro d). En la esfera también será un círculo, pero su radio dependerá de la distancia d. Mirando la figura siguiente y acordándote del teorema de Pitágoras, fácilmente puedes escribir que si el radio de la sección es r, entonces:

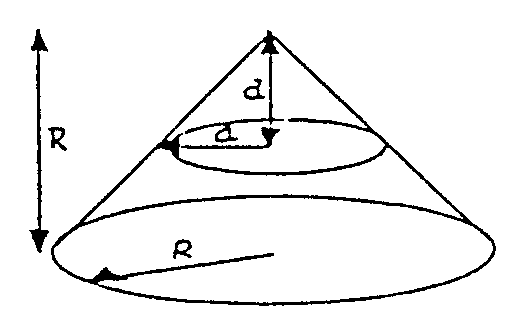
En el cono la sección también será un círculo y ahora el radio es aún más fácil de determinar mirando a la figura siguiente
Como el radio de apertura del cono es de 45º, resulta que el radio es d. Así :

Las secciones son como rebanadas de las tres figuras obtenidas cortando paralelamente a la base del cilindro. Resulta que, colocando las tres figuras como las hemos puesto y cortándolas en rebanadas finas tendremos

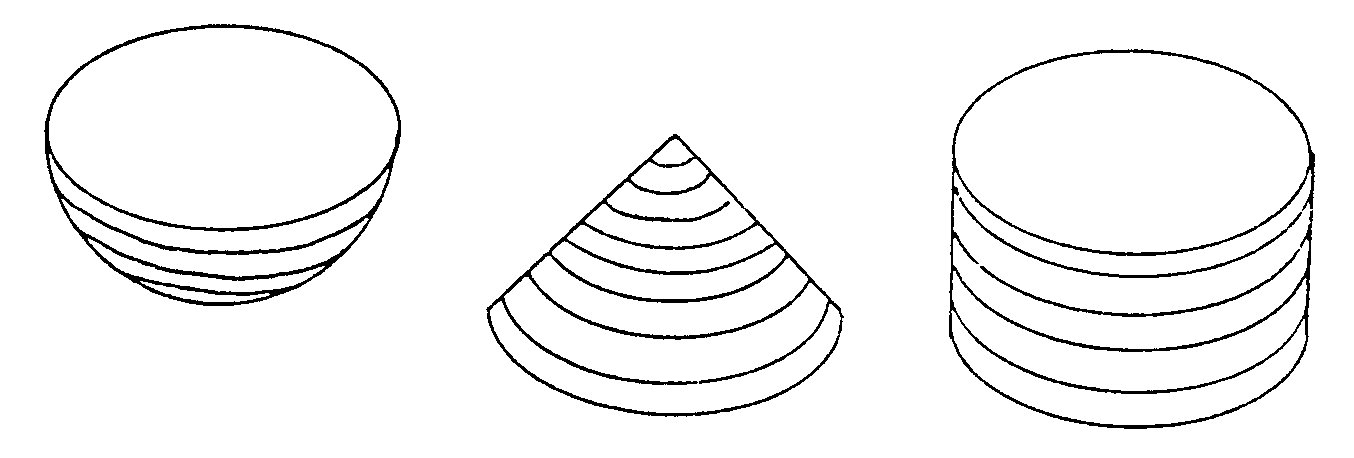
Rebanada en cilindro a altura d = Rebanada en semiesfera + Rebanada en cono.

Si para cada altura d se tiene esta relación, parece bastante claro que:
Volumen cilindro = Volumen semiesfera + Volumen cono
Pero, como Arquímedes muy bien sabía: